 |  | |
|
УДК 528.441.21 К вопросу совершенствования мониторинга земельных ресурсов
Басова И.А., профессор, Липская Е.О., ст.преподаватель Тульский государственный университет, Россия
Рассматриваются методологические вопросы объективной оценки состояния и качества земельных ресурсов с учетом неоднородности пространственного загрязнения почвенного покрова по данным наземного мониторинга. Первостепенное значение для обработки значительных информационных баз данных и прогнозирования результатов по качественной оценке состояния земельных ресурсов имеет выбор математического аппарата, пригодного для объективного описания свойств загрязнения почвенного покрова, приобретенных вследствие антропо-техногенного загрязнения, установления параметров изменения этих свойств.
Актуальность исследования Земельные ресурсы, являясь важнейшей составной частью природной среды, пространственным базисом для размещения народнохозяйственных объектов и расселения людей, главным средством производства в сельском хозяйстве характеризуются различными параметрами, такими как территория, климат, рельеф, качество почв, гидрологический режим, растительность и другими признаками. Обеспечение объективной оценки состояния и качества земельных ресурсов, как одной из главных задач рационального и эффективного их использования, предполагает комплексное изучение и анализ природных факторов, определение антропогенной нагрузки и последствий хозяйственной деятельности человека[1]. Особенную роль в аспекте охраны ресурсов занимает почвенный покров. Он, устойчиво аккумулируя в себе все изменения, происходящие в биогеоценозах и биосфере, на длительных отрезках географической среды, является естественной базой для жизни людей, и служит не только основой для создания рекреационных зон и формирования экологической обстановки для жизненного пространства, но и «инфицирует» риск различных заболеваний. Перспективы решения комплексной оценки природно-ресурсного потенциала территории требуют четкого разграничения компетенций в области управления природными ресурсами между субъектами Российской Федерации в связи с децентрализацией экономики. Государственное управление этим процессом невозможно без полной информации о количестве, качестве и экологической оценке отдельных видов природных ресурсов в границах каждого административно-территориального образования. Для разработки планов рационального использования земельных ресурсов на различных уровнях административного управления в настоящее время активно идет формирование информационных баз данных по учету земельных ресурсов и оценке их изменения под воздействием природно-техно-антропогенных нагрузок. Однако рассредоточение функций между административными службами затрудняет эффективное использование земель, а отсутствие методологии эколого-экономической оценки земли ведет к дефициту в бюджете и не позволяет целенаправленно формировать инвестиционную политику для совершенствования системы землепользования и землеустройства территорий. Одним из основных источников ухудшения состояния земельных ресурсов, и прежде всего по твердым отходам, являются предприятия черной и цветной металлургии, угольной промышленности и других отраслей, занимающихся освоением топливно-энергетических и минеральных ресурсов. В целях экологической безопасности освоения недр реализуется Концепции государственной стратегии взаимодействия человека с окружающей средой [1]. Это обуславливает необходимость методически обоснованного подхода к решению проблем рационального использования и охраны земельных ресурсов, в том числе с учетом реальных характеристик пространственно-временной неоднородности загрязнителей, блочного характера структуры почвы, региональными и локальными особенностями ее свойств.
Основное содержание Первостепенное значение для обработки значительных информационных баз данных и прогнозирования результатов по качественной оценке состояния земельных ресурсов имеет выбор математического аппарата, пригодного для объективного описания свойств загрязнения почвенного покрова, приобретенных вследствие антропо-техногенного загрязнения, установления параметров изменения этих свойств. При построении моделей состояния почвенного покрова (далее экологического поля) на региональном уровне часто оперируют статистическими моделями, содержащими различные параметры показателей состояния почв – морфологических, химических и т.д. В наземном мониторинге для анализа загрязнения почвенного покрова выполняют взятие проб (опробование). Такой мониторинг имеет сугубо дискретный характер. При этом, меняющаяся пространственная переменная загрязнителя принимает дискретные значения, причем совокупность этих значений конечна. Простейшей гипотезой, которую можно выдвинуть относительно колеблющегося ряда пространственных переменных, является предположение о том, что колебания случайны [2]. В литературе достаточно широко рассматриваются предложения по количественному анализу исходной информации для принятия или непринятия гипотезы о случайности замеров признака с точки зрения периодичности их в пространстве [3,4,5]. Статистические методы для количественной оценки экологического состояния почвенного покрова по загрязнению по данным мониторинга могут быть использованы только при определенных условиях. Критерием, определяющим эти условия, является соотношение расстояний между точками взятия проб на анализ загрязнителя и размерами морфологических элементов. Если расстояния между пробами больше поперечников элементов, замеры обладают всеми свойствами случайных величин. Эти методы, несмотря на очевидные достоинства применения в приложениях, не дают ответа на вопрос о характере закономерностей в изменчивости признака, если они существуют. Выявление морфологических закономерностей моделей пространственного размещения загрязнителей позволяет создавать эффективные методы прогнозной оценки состояния почвенного покрова земельных ресурсов. Для оценки закономерности пространственной изменчивости какого-либо признака (загрязнителя) широко используется теория одномерного тренда, которая состоит в анализе скачков (переходы через средний уровень значений признака) или критерий Спирмена для дихотомических последовательностей [7,8]. Теория одномерного тренда состоит в расчете количественного критерия, разграничивающего последовательности с закономерным или случайным распределением элементов, чисел или точек опробования. Разграничительным критерием является вероятность наличия точек смены знака или числа скачков в дихотомической последовательности. Термину «скачок» соответствует последовательность из одного или нескольких элементов, в которой значения каждого последующего элемента монотонно возрастают (скачок вверх) или убывают (скачок вниз). При количестве точек более 10 пользуются приближенным распределением структурных элементов ряда к нормальному закону с параметрами: математическим ожиданием числа скачков, математическим ожиданием числа точек смены знака, дисперсией для обоих случаев: Значения вероятностей в соответствии с нормированными отклонениями, которые определяются по таблицам значений функций Лапласа для нормального закона распределения вероятностей, считаются значимыми, если их значения превышают вероятность 0,05, т.е. последовательность наблюдаемых точек следует считать случайной. В противном случае принимается гипотеза о наличии закономерности в распределении элементов. Условия случайности или закономерности изменчивости наблюдаемого признака определяются степенью изученности действительной поверхности. При малых расстояниях между точками измерений изменчивая поверхность аппроксимируется без ошибки аналогии и последовательность точек следует считать закономерной. При увеличении расстояний между замерами выявляются существенные погрешности аппроксимации морфологических элементов. Изучаемая поверхность сглаживается, теряются отдельные детали морфологии, что особенно негативно в условиях предельных загрязнений. При ограниченной информации мониторинга загрязнителей почвенного покрова земельных ресурсов в качестве основного оператора анализа закономерностей изменчивости признака, вида и степени проявления закономерностей, если они существуют, выявление отсутствия явно выраженных закономерностей, а, следовательно, случайность изменчивости признака может использоваться средняя величина D// ср вторых последовательных разностей
(D//i=ABS((ti-ti+1) – (ti+1-ti+2)) )
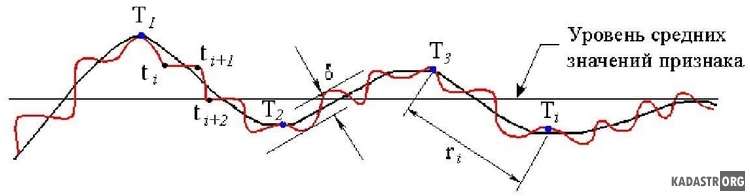
между соседними замерами признака, расположенными на кратчайшем расстоянии друг от друга (рисунок 1). [9,10 ]
Рисунок 1- Формирование вторых разностей по случайным замерам признака: Ti- точки смена знака значения признака, ti- текущие замеры признака, d- не выявляемая амплитудная изменчивость признака, ri- дихотомические "скачки" признака
По результатам анализа многочисленных вариантов сочетаний последовательных разностей было установлено, что величина D// весьма чувствительна к наличию закономерностей в пространственном положении признака и более четко характеризует особенность изменчивости, которая выражается числом скачков в дихотомической последовательности. [10]. Поскольку массивы значений D//ср. и числа скачков были достаточно велики, обработка полученных множеств производилась с использованием методов математической статистики. Результаты обработки представлены графиком эмпирического распределения средних величин вторых последовательных разностей (Рисунок 2).
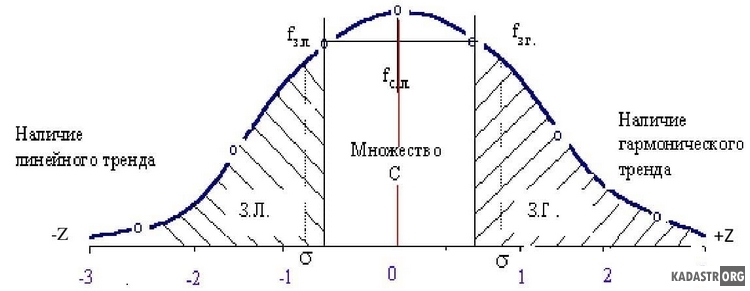
Рисунок 2 - Функция F(D//) эмпирического распределения значений вторых разностей и аппроксимация его нормальным распределением: fi– вероятности закономерных сочетаний признака; З.Л., З.Г.– области линейных и гармонических закономерностей; Z–нормированная величина отклонения от среднего уровня; Z(-1),Z(+1) – квантили, ограничивающие множество «С» случайных сочетаний значений признака.
Функция распределения хорошо аппроксимируется нормальным законом с параметрами:
М= (D//max)/2, D(D//)= ( D//ср.max)2/3s
Это обстоятельство оказывается важным для оценки параметров распределения D//ср по результатам первичных материалов мониторинга Область левее ординаты fз.л. характеризуется низкими значениями D//ср , что связано с наличием преимущественно линейной зависимости в изменчивости признака. Область справа от ординаты fз.л. соответствует наличию закономерностей, характеризующихся периодическими изменениями типа гармонических колебаний.
Множества значений D//ср , соответствующие наличию закономерностей в изменчивости признака ( З.Л. и З.Г. ), пересекаются в узких зонах справа и слева со множеством С области случайных сочетаний замеров. Это указывает на неопределенность принятия решений о случайном или закономерном характере изменчивости признака, когда средние значения вторых разностей совпадают с граничными зонами, что объясняется отсутствием четкой границы между понятиями случайности и закономерности, поскольку все зависит от уровня принятых допущений и точности анализа. При анализе результатов мониторинга нет необходимости стремиться к точности, превышающий уровень погрешности измерений. Для удовлетворительного решения достаточно принять в качестве значимого критерия плотности вероятностей fi, расположенные симметрично от математического ожидания, на односигмовых расстояниях, совпадающих с зонами пересечения множеств С, ЗП, ЗГ. Плотность вероятностного распределения fi множества средних значений вторых последовательных разностей в каждом конкретном случае может быть найдена по таблицам нормального распределения в соответствии с нормированным отклонением
Z= (D//ср -M(D//ср)/s D//ср =(D//ср -`D//ср)/ s D//ср, s D// =Ö D(D//ср)
где D//ср – средняя величина вторых разностей анализируемой совокупности; М(D//ср)– математическое ожидание распределения средних значений вторых последовательных разностей; `D//ср– оценка величины М(D//ср), sD// –среднеквадратическое отклонение. Если значение Z попадает в интервал ± 1, то совокупность замеров признака можно считать набором случайных величин, а особенности их вероятностного распределения статистически подконтрольными. Иначе принимается гипотеза о наличии закономерностей, причем при Z, соответствующих отрицательным значениям, исследуемая совокупность характеризуется наличием линейной закономерной изменчивостью. Если значения Z положительны, то закономерная изменчивость признака доминирует над случайной. В этом случае она характеризуется наличием периодических изменений типа гармонических колебаний. В обоих случаях при наличии закономерностей необходимо отказаться от статистических методов оценки изменчивости объекта. На основе углубленного анализа данных мониторинга необходимо подобрать соответствующую математическую модель, и использовать ее вместо статистических характеристик, которые в данном случае дают значительно меньше информации о действительной изменчивости признака. В соответствии с рекомендациями американских исследователей, гипотеза о случайном виде изменчивости представленной модели принимается, если величина нормированного отклонения Z функции распределения скачков меньше ±1,95. [2] Можно отметить, что принятие гипотез об изменчивости частных реализаций экологического поля загрязнения зависит не столько от нерегулярности морфологии моделей, сколько от достоверности их воспроизведения, т.е. от плотности замеров.
Выводы Если подтверждается вывод о наличии закономерностей в морфологии поля загрязнения по данным уплотнённого профиля, то это позволяет применить далее информативные способы выражения её изменчивости. Представленный алгоритм отличается исключительной простотой и высокой чувствительностью. Однако, целесообразнее использовать для анализа дихотомические последовательности. Исследование наблюдений по точкам смены знака менее предпочтителен, так как этот метод более формален и учитывает мелко амплитудную изменчивость высоких порядков, не играющих роли при описании геометрии загрязнения. Принятие решения для использования адекватного математического аппарата при обработке мониторингов тяжелых металлов требует проверки гипотезы о случайном или закономерном изменении содержания загрязнителя в пространстве. Для решения задачи можно использовать результаты статистического анализа вторых разностей. Критерием разграничения закономерных и случайных сочетаний в наборе вторых разностей может быть принята нормированная величина односигмового интервала. При этом, степень случайности в последовательности замеров зависит не от регулярности пространственного размещения загрязнителя, а от достоверности воспроизведения морфологии геоэкологического поля. Процедура степени неоднородности загрязнения изучаемого объекта должна начинаться с подготовки базы исходных данных, которая в самом начале анализируется на информационный статус, определяющий принципы адекватного математического моделирования.
Библиографический список
| ||
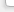 | 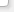 |