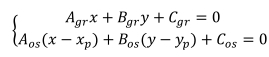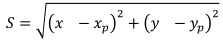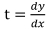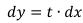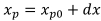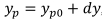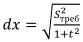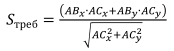 |  | |||||||||||||||||||||||||||||
|
УДК 528.486.1 Алгоритм формирования ведомости полосы отвода автомобильной дороги для ЭВМ
Маляренко А.Д., кадастровый инженер ГАУ ТО «Проектная контора», Россия
Показана идея автоматизации вычисления ширины полосы отвода, как коридора линий.
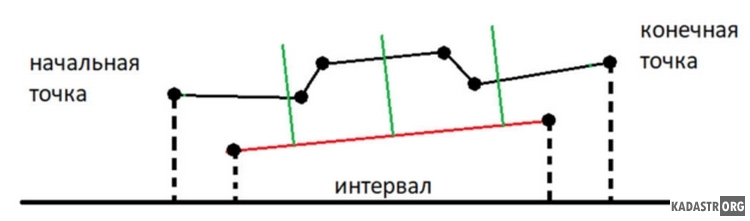
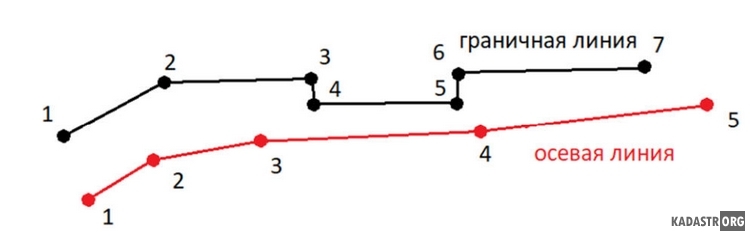
При эксплуатации автомобильных дорог возникает проблема определения ширины территории обслуживания, в пределах которой необходимо вести расчистку древесно-кустарниковой растительности. Удобным вариантом представления информации о ширине полосы отвода является ведомость, в которой расстояния от начальной точки и ширина поставлены в соответствие. Ширину полосы отвода представим в виде суммы правой и левой половин расстояний от осевой линии. Модель для вычислений представляет собой коридор, составленный из прямых линий осевой, граничной и перпендикулярной к осевой.
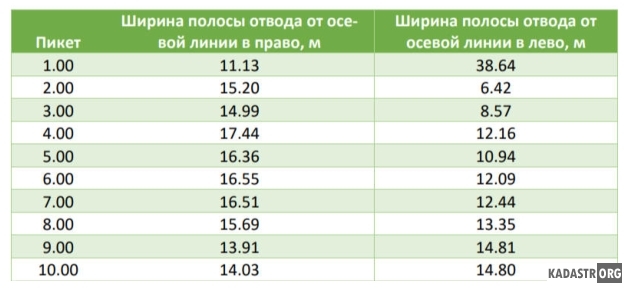
Таблица 1 - Структура исходных данных
Рисунок 1 - Модель для вычислений
Уравнение прямой линии на плоскости задается общим уравнением вида: Ax+By+C=0 [1, c. 50]. Исходя из структуры такое уравнение составляется на осевую линию и на граничную.
На отрезке осевой линии:
На отрезке граничной линии:
Уравнение перпендикуляра к прямой: где xp,yp – координаты точки, расположенной на осевой линии. Находится точка пересечения прямых и перпендикулярных линий решая систему уравнений
Получены координаты x,y По теореме Пифагора находится расстояние между точками осевой линии, через которую проведен перпендикуляр и точкой по координатам из системы уравнений (4).
Где x и y – координаты точки из решения системы уравнений Циклический алгоритм позволяет вычислять данное значение для множества точек граничной и осевой линии. При вычислениях возможны варианты развития ситуации:
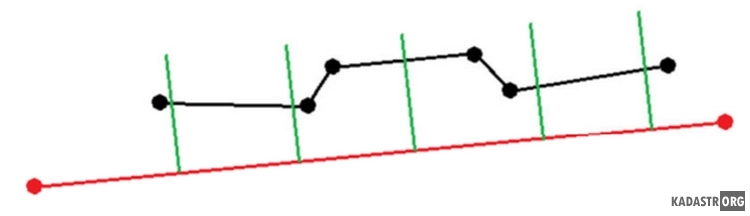
Ниже приведена иллюстрация второго варианта.
Рисунок 2 - Превышение количества точек граничной линии относительно количества точек осевой.
При недостатке точек на осевой линии точку с координатами (xp; yp) необходимо сдвигать по линии на определенный шаг, рассчитываемый из соотношения приращений координат:
Вычислив t можно выяснить величину изменения dy относительно произвольного dx:
Смещенные координаты точки вычисляются через приращения dx, выбранное произвольно, и dy, вычисленное по формуле (7):
Знаки вычисленных приращений координат выбираются такими же как и знаки приращений координат линии при вычислении соотношения (6). Частным случаем является вертикальная и горизонтальная прямая, для которой не вычисляется соотношение (6), а сразу добавляется приращение по x в случае вертикальной прямой или по у в случае горизонтальной.
Приращение dx в зависимости от требуемого расстояния Sтреб на линии вычисляется по формуле:
Приращение dy вычисляется по формуле (7). Таким образом обеспечивается подвижность точки проведения перпендикуляра от начальной до конечной точки отрезка осевой линии.
Рисунок 3 - Выход за интервал начальной и конечной точек граничной линии
Точка xp,yp осевой линии находится вне интервала начальной и конечной точек граничной линии Возникает вопрос о том, на сколько надо сдвигать точку, чтобы она попадала в интервал. Для этого обратимся к векторам на рис. 4.
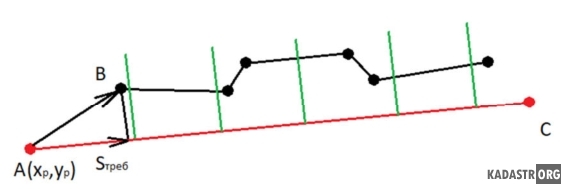
Рисунок 4 - Векторы для определения сдвига точки по линии
На данном рисунке изображены векторы AB и AC. Спроецируем вектор AB на вектор AC и получим компоненты вектора-проекции, из которых найдем по теореме Пифагора расстояние Sтреб . Проекция вектора
ABx – компонента x вектора AB; ABy– компонента y вектора AB; ACx– компонента x вектора AC; ACy – компонента y вектора AC.
Рисунок 5 - Готовая ведомость.
Выводы Предложенный алгоритм автоматического формирования ведомости полосы отвода позволяет многократно сократить временные затраты на ее составление. Ручная обработка ведомости имеет большую трудоемкость, что вызвано измерением каждого отрезка вдоль всей линии, которая может иметь большую длину. Сформирован алгоритм подвижности точки на осевой линии, позволяющий определять ширину полосы отвода при различном шаге ведомости, в зависимости от требований потребителя. Выявлены возможные варианты исходных данных и способы их обработки.
Библиографический список:
| ||||||||||||||||||||||||||||||
 |  | |||||||||||||||||||||||||||||
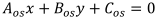 , (1)
, (1)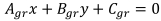 ., (2)
., (2)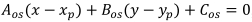 , (3)
, (3)