 |  | |||||||||||||||||||||||||||||||
|
УДК 528.2/.5 Решение задачи трансформирования систем координат с учетом наложения условий
Дегтярёв А.М., доцент, Ивашнёва А.С., аспирант Полоцкий государственный университет им. Евфросинии Полоцкой, Белоруссия
Рассмотрены возможные модели трансформирования систем координат и предложено решение задачи трансформирования с учетом наложения условий для перехода от одной модели к другой.
Объединение данных, относящихся к разным системам координат, является важным с точки зрения геодезии средством обеспечения совместимости данных. Эта унификация данных обычно осуществляется посредством соответствующих операций с координатами. Задача двумерного трансформирования может решаться в случае перехода координат от одной государственной системы в другую; при выполнении кадастровых работ; при выносе в натуру проектов сооружений; когда определяются элементы деформации различных объектов; выполняются фотограмметрические работы и т.д. В зависимости от состава элементов преобразования можно выделить следующие модели планового преобразования координат: твердотельная, конформная, аффинная. Рассмотрим шесть элементов двумерного преобразования: tx, ty – сдвиги по осям X, Y, соответственно,φ – угол поворота осей одной координатной системы относительно другой, mх, mу – величины изменения масштабов по осям X, Y, соответственно, ε – угол неортогональности между осями двух координатных систем. В зависимости от того, какая модель преобразования, в коэффициентах будет содержаться определенный набор элементов. В случае конформной модели выполняется разворот точек на угол φ, сдвиги по осям на величины tx и ty и равномерно изменяется масштаб на величину m по формулам:
или в другом представлении, когда элементы скрыты в коэффициентах [1]
где a, b, c, d - преобразующие коэффициенты; XH, YH - координаты общей точки в новой системе; XC, YC - координаты этой же точки в старой системе. В случае аффинной модели производиться сдвиг по осям на величины tx и ty, изменяется масштаб на величины mх и mу, выполняется поворот относительно одной оси на угол φ1, а другой, на другой угол φ2 = φ1 + e, т.е. с нарушением ортогональности исходной системы координат, по формулам:
или в другом представлении, когда элементы скрыты в коэффициентах
где a, b, c, d, e, f - преобразующие коэффициенты. Аффинная и конформная модели широко используется для трансформирования плоских систем координат. Существует возможность использовать аффинную модель как более универсальную, а при необходимости осуществлять переход к конформной модели. Рассмотрим процедуру решения задачи трансформирования с учетом наложения условий для перехода от аффинной к конформной модели. При реализации алгоритма аффинного трансформирования часто все неизвестные вытягиваются в вектор и решение производиться на основе метода наименьших квадратов. Решение на основе данного подхода описано во многих источниках (см., например, [2]). Для наложения условий на аффинную модель, исходя из уравнений (2) и (4) можно задать условия для перехода следующим образом:
тогда
Преобразовываем матрицу коэффициентов системы нормальных уравнений к виду
где А – матрица плана [2], Z – нулевая матрица второго порядка. А матрица В формируется на основе условий (6) посредством взятия частных производных по коэффициентам a, b, c, d, e, f и имеет вид
также вектор свободных членов принимает вид
Далее находим вектор неизвестных как
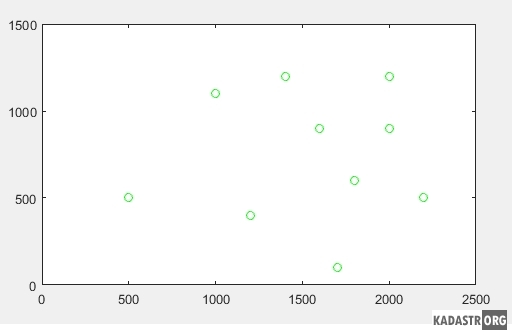
В ходе вычислительного эксперимента стояла задача, закладывая различные модели трансформирования, осуществить переход от аффинной модели к конформной через предложенную выше процедуру. Для реализации закладывались аффинная и конформная модели. Данные для вычислительного эксперимента моделировались следующим образом. Были сформированы координаты десяти точек, расположенные равномерно (Рисунок 1).
Рис. 1 – Расположение общих точек в первой системе координат
Затем в зависимости от заложенной модели по элементам преобразования, координаты пересчитывались из старой системы координат в новую систему. Для аффинной модели использовались такие элементы преобразования как угол поворота равные 30°, угол неортогональности 3°, масштабные коэффициенты 1 и 2, сдвиги по осям 100 м и 200 м. Для конформной модели использовались такие элементы преобразования как угол поворота равные 30°, масштабный коэффициент 1.2, сдвиги по осям 100 м и 200 м. По полученным двум наборам координат проводилась обратная процедура, предполагалось, что заложенная модель неизвестна, и коэффициенты вместе с элементами трансформирования вычислялись исходя из предположений: первое, модель аффинная, второе, модель конформная. Далее осуществлялся переход по предложенной процедуре с помощью наложения условий от аффинной модели к конформной модели. Сравнивались элементы, полученные по конформной модели с элементами, полученными по аффинной модели с условиями. Полученные результаты представлены в Таблице 1 и в Таблице 2.
Таблица 1 - Коэффициенты и элементы трансформирования (заложена конформная модель)
Таблица 2 - Коэффициенты и элементы трансформирования (заложена аффинная модель)
Полученные таким образом результаты, показали, что с помощью наложения условий возможно осуществить переход от аффинной модели к конформной, получив такие же элементы трансформирования. Данная процедура дает результат не зависимо какая модель изначально заложена.
Библиографический список
| ||||||||||||||||||||||||||||||||
 | 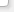 | |||||||||||||||||||||||||||||||
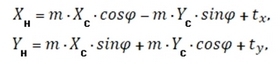 (1)
(1)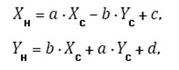 (2)
(2)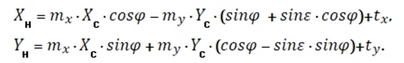 (3)
(3)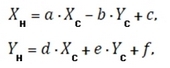 (4)
(4)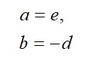 (5)
(5)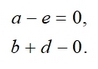 (6)
(6)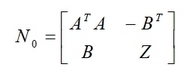 (7)
(7) (8)
(8)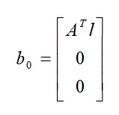 (9)
(9)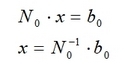 (10)
(10)