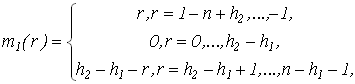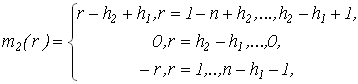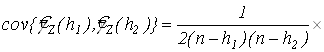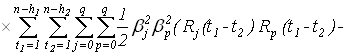| |

УДК 519.24
Исследование асимптотических свойств оценки семивариограммы гнездовой структуры
Цеховая Т. В., доцент, Кисель А. Ю., студентка
Белорусский государственный университет, Беларусь
Рассмотрен случайный процесс с неизвестной семивариограммой гнездовой структуры. Построена оценка семивариограммы и исследованы ее статистические свойства. Полученные результаты проверены на модельных данных, используя возможности языка Python.
В настоящее время для решения ряда прикладных задач прогнозирования в геологии, гидрологии, экологии, природопользовании, здравоохранении, почвоведении и других областях находят широкое применение геостатистические методы. Ключевым понятием геостатистики является семивариограмма. В связи с этим актуальны задачи исследования свойств этой функции, а также построения и изучения ее оценок [1-4].
В данной работе рассматривается случайный процесс с семивариограммой гнездовой структуры. Процесс такого вида является математической моделью, адекватно воспроизводящей изменения во многих сложных системах окружающего мира [5].
Пусть
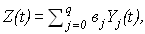 (1) (1)
где 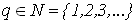 , , 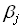 - постоянные, удовлетворяющие условию: - постоянные, удовлетворяющие условию:
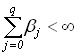
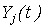 – гауссовские случайные процессы с математическим ожиданием – гауссовские случайные процессы с математическим ожиданием 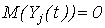 и неизвестными ковариационными функциями и неизвестными ковариационными функциями 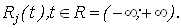
Предположим также, что взаимные ковариационные функции 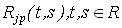 случайных процессов случайных процессов 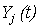 и и 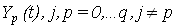 , удовлетворяют равенству: , удовлетворяют равенству:
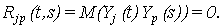
Теорема 1. Случайный процесс 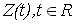 , является стационарным в широком смысле. , является стационарным в широком смысле.
Доказательство теоремы приводится в статье [5].
Заметим, что для стационарного в широком смысле случайного процесса ковариационная функция 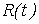 и семивариограмма и семивариограмма 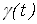 связаны соотношением [1]: связаны соотношением [1]:
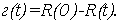 (2) (2)
Теорема 2. Семивариограмма случайного процесса 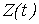 имеет представление: имеет представление:
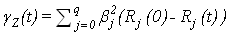 , (3) , (3)
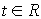 . .
Доказательство теоремы приводится в работе [5].
В качестве оценки семивариограммы стационарного в широком смысле случайного процесса 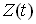 , построенной по последовательным полученным через одинаковые промежутки времени наблюдениям , построенной по последовательным полученным через одинаковые промежутки времени наблюдениям 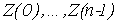 , рассмотрим статистику вида: , рассмотрим статистику вида:
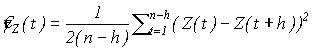 , (4) , (4)
где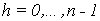 . Положим также . Положим также 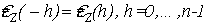 , и , и 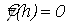 для для 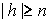 . .
C помощью возможностей языка программирования Python построим оценку (4) семивариограммы.
Предположим, что 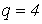 , а случайные процессы , а случайные процессы 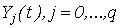 , имеют соответственно ковариационные функции , имеют соответственно ковариационные функции
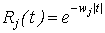 , ,
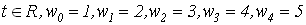 . .
Тогда из соотношения (2)
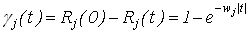 . .
Принимая во внимание утверждение теоремы 2, семивариограмма процесса 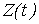 будет иметь вид: будет иметь вид:
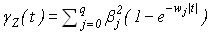 . (5) . (5)
Смоделируем по 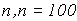 , наблюдений , наблюдений 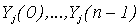 за случайными процессами за случайными процессами 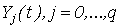 . Далее, полагая . Далее, полагая 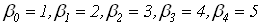 , и учитывая (1), вычислим , и учитывая (1), вычислим 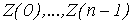 . .
Применяя пакет matplotlib, построим графики семивариограммы (5) и ее оценки (4). На рисунке 1 график оценки семивариограммы 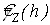 представлен зеленым цветом, а график истинной семивариограммы представлен зеленым цветом, а график истинной семивариограммы 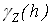 изображен оранжевым. изображен оранжевым.
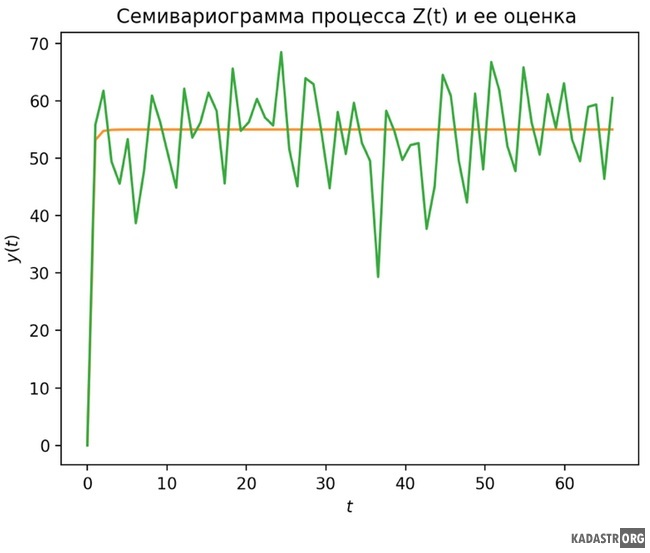
Рис. 1 – Семивариограмма 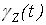 и ее оценка и ее оценка 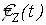 для для 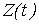
Найдем выражения для первых двух моментов оценки семивариограммы случайного процесса 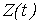 . .
Нетрудно показать, что
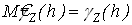 , (6) , (6)
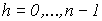 , т. е. статистика (4) является несмещенной оценкой семивариограммы. , т. е. статистика (4) является несмещенной оценкой семивариограммы.
Теорема 3. Для оценки семивариограммы 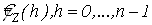 , случайного процесса , случайного процесса 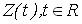 , имеют место следующие соотношения: , имеют место следующие соотношения:
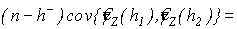
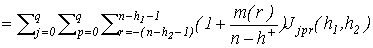 , (7) , (7)
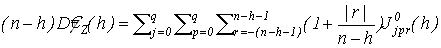 , (8) , (8)
где
 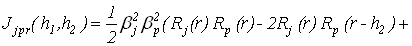
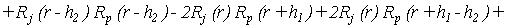
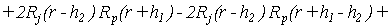 (9) (9)
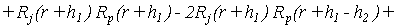
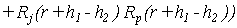 , ,
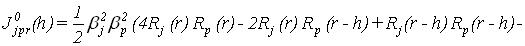
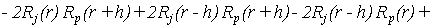 (10) (10)
 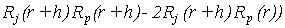 , ,
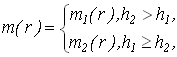 (11) (11)
 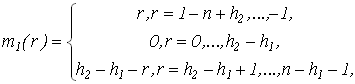
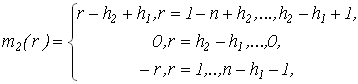
 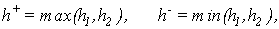 (12) (12)
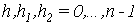 . .
Доказательство. В работе [5] было показано, что
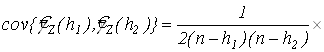
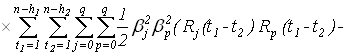
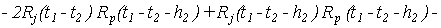
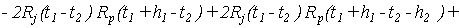
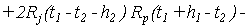
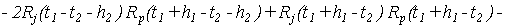
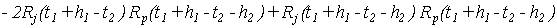 . .
Сделаем замену переменных 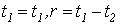 и изменим порядок суммирования. Тогда, учитывая (9), (11) и (12), получим выражение (7) для ковариации. и изменим порядок суммирования. Тогда, учитывая (9), (11) и (12), получим выражение (7) для ковариации.
Равенство (8) для дисперсии оценки семивариограммы (4) нетрудно получить из (7), если положить 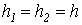 и принять во внимание (10). и принять во внимание (10).
Исследуем асимптотическое поведение вторых моментов оценки семивариограммы 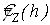 при дополнительных ограничениях на характеристики процессов при дополнительных ограничениях на характеристики процессов 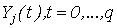 , во временной области. , во временной области.
Теорема 4. Если имеет место:
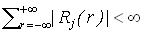 , (13) , (13)
где 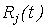 – ковариационные функции случайных процессов – ковариационные функции случайных процессов 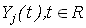 , соответственно, то , соответственно, то
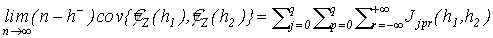 , (14) , (14)
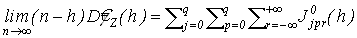 , ,
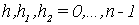 , , 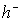 определено равенством (12), определено равенством (12), 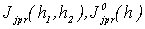 - задаются выражениями (9), (10) соответственно. - задаются выражениями (9), (10) соответственно.
Доказательство. Учитывая (7) рассмотрим разность
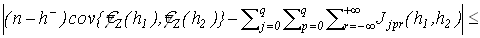
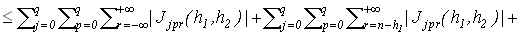
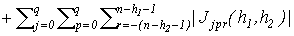 , ,
где 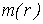 задается равенством (11), задается равенством (11), 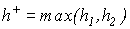 . .
Обозначим слагаемые в правой части последнего неравенства соответственно 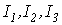 . Поскольку имеет место (13), то . Поскольку имеет место (13), то 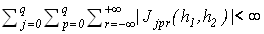 . Следовательно, слагаемые . Следовательно, слагаемые 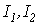 стремятся к нулю при стремятся к нулю при 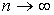 как остаток сходящегося ряда, а как остаток сходящегося ряда, а 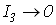 при при 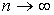 в силу леммы Кронекера [7]. Таким образом, справедливо (14). в силу леммы Кронекера [7]. Таким образом, справедливо (14).
Второе утверждение теоремы доказывается аналогично, если положить 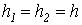 . Теорема доказана. . Теорема доказана.
Из теоремы 4 следует, что
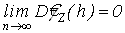 , (15) , (15)
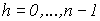 . .
В силу (6) и предельного равенства (15) можно сделать вывод, что 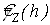 является состоятельной в среднеквадратическом смысле оценкой для семивариограммы является состоятельной в среднеквадратическом смысле оценкой для семивариограммы 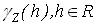 . .
Библиографический список:
-
Cressie N. Statistics for Spatial Data. – New York. – Wiley, 1991. – 900 p.
-
Цеховая Т.В. Свойства вариограммы внутренне стационарных случайных процессов // Теория вероятностей, математическая статистика и их приложения. Материалы научной конференции. Минск: БГУ. 2004. С. 181-186.
-
Труш Н.Н., Цеховая Т.В. Исследование статистических свойств оценок вариограммы и ковариационной функции // Вести НАН Беларуси. Сер.1, Физ. Мат. Мех., №2, 2001, С. 24-29.
-
Troush, N. N.Tsekhavaya, T. V. The Variogram Estimates Of The Intrinsically-Stationary Stochastic Processes And Fields // MS'2004. International Conference on Modelling and Simulation, Minsk, Belarus, 27-29 April, 2004/ Minsk, BSU. P. 258-261.
-
Цеховая, Т.В. Первые два момента оценки семивариограммы случайного процесса с семивариограммой гнездовой структуры / Т.В. Цеховая, А.Ю. Кисель // III Международная научно-практическая конференция “НАУКА И ОБРАЗОВАНИЕ В СОВРЕМЕННОМ МИРЕ: ВЫЗОВЫ ХХI века”. Нур-Султан, Казахстан, 10-12 июля 2019г. / Қҧраст.: Е. Ешім, Е. Абиев т.б. – Нур-Султан, 2019. Т. IV, С. 48 – 51.
-
Taylor C. C., Burаrough P. A. Multiscale Sources of Spatial Variation in Soil. III. Improved Methods for Fitting the Nested Model to One-dimensional Semivariograms. Mathematical Geology, Vol. 18, No. 8, 1986. P. 811-821.
-
Ширяев, А. Н. Вероятность / А. Н. Ширяев. – 4-е изд. – Москва, МЦНМО, 2007. – 577 с.
| |
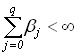
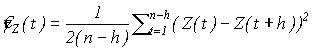 , (4)
, (4)
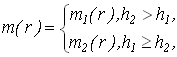 (11)
(11)