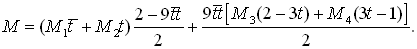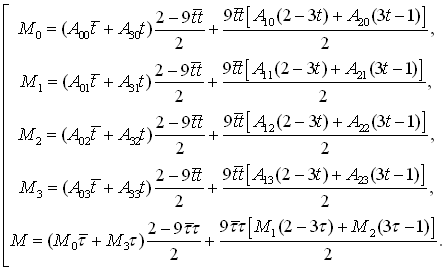 |  | |||||||
 УДК 004.94 Создание цифровых моделей рельефа местности в БН-исчислении
Конопацкий Е.В., доцент, Чернышева О.А., ассистент Донбасская национальная академия строительства и архитектуры
Рассмотрена разработка вычислительных алгоритмов создания цифровых моделей рельефа местности, которые представляют универсальный инструмент моделирования участка нерегулярной топографической поверхности, состоящей из регулярных криволинейных 16-точечных отсеков.
Аналитическое и компьютерное моделирование участка топографической поверхности относится к задачам определения цифровых моделей рельефа местности и является неотъемлемой составляющей современных геоинформационных систем, а также активно используется в горном деле, геодезии, картографии, землеустройстве, навигации, строительстве и т.д. На данный момент методы геометрического моделирования участка топографической поверхности по способу аппроксимации можно разделить на две категории: линейные и криволинейные. К линейной аппроксимации относятся различные способы триангуляции, преимуществом которых является возможность моделирования участка топографической поверхности на нерегулярной сети точек. Недостатком является значительное искажение формы топографической поверхности при больших расстояниях между исходными точками сети. К криволинейной аппроксимации можно отнести сплайновые методы моделирования топографической поверхности, которые более точно передают криволинейную форму топографической поверхности, но при этом их построение возможно исключительно на основе регулярной сети точек, а если исходная сеть имеет нерегулярный характер, то приходится выполнять дополнительную операцию – переход от нерегулярной сети точек к регулярной. Чтобы исключить необходимость такого перехода, возникает задача аппроксимации участка топографической поверхности криволинейной поверхностью, которая при этом может быть использована на нерегулярной сети точек без предварительной их обработки. В этой связи совершенствование методов геометрического моделирования топографической поверхности на базе новых вычислительных алгоритмов и современных компьютерных средств является актуальной научно-практической задачей, имеющей отраслевое значение. Анализ существующих методов определения цифровых моделей рельефа местности (ЦМР), который показал, что все существующие способы можно разделить на 2-е группы: Первая группа – способы, основанные на нелинейной интерполяции высот с использованием полиномов, сплайнов, корреляционных функций и т.п.: − кусочно-полиномиальный способ [1-2]; − способы, основанные на применении рядов Фурье [3]. Вторая группа − способы, основанные на построении геометрически упорядоченной (регулярной или нерегулярной) модели, элементами которой являются либо упорядоченные линии, либо поверхности различных многогранников: − Цифровая модель TIN [4-5]; − Цифровая модель DEM [6]; − Фотограмметрическая технология построения цифровой модели [7]. Несмотря на значительный объем исследований и наличие широкого спектра программных продуктов в области создания цифровых моделей рельефа местности, на данный момент отсутствует единый, математически обоснованный подход, позволяющий моделировать криволинейные участки топографической поверхности на нерегулярной сети точек без предварительной обработки исходных данных, которая заключается в переходе от нерегулярной сети точек к регулярной. Наиболее простыми и изученными криволинейными формами являются кривые 2-го порядка, которые позволяют строить ЦМР состоящие из 9-точечных отсеков, на основе регулярной сети точек с помощью параболической, эллиптической и гиперболической интерполяции. Однако на нерегулярной сети точек без предварительной обработки данных такой способ моделирования не может быть использован. Для аппроксимации участка топографической поверхности на основе нерегулярной сети точек необходима линия двоякой кривизны, наиболее простой из которых, является дуга кривой Безье 3-го порядка:
где
Модифицировав уравнение (1), чтобы дуга кривой Безье 3-го порядка проходила через 4 наперёд заданные точки
Воспользуемся полученным точечным уравнением модифицированной дуги кривой Безье 3-го порядка для конструирования отсека криволинейной поверхности. Для унификации будем использовать одно и то же уравнение (2). Тогда для построения образующей необходимо иметь 4 направляющие линии (по количеству текущих точек). Если каждая из направляющих будет определяться уравнением (2), то в итоге получим вычислительный алгоритм построения отсека топографической поверхности, проходящий через 16-ть наперёд заданных точек:
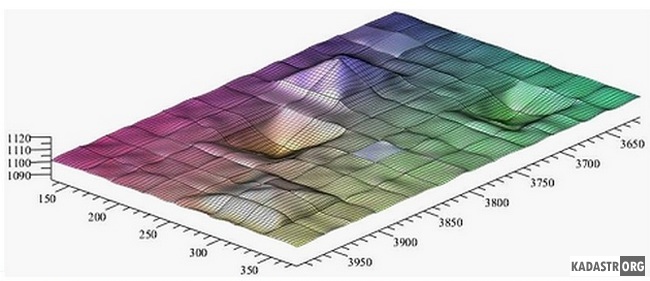
Предложенный вычислительный алгоритм [8] прошёл успешную апробацию при создании ЦМР, как на регулярной, так и на нерегулярной сети точек. В качестве примера рассмотрим ЦМР на регулярной сети, состоящей из 96-ти 16-точечных отсеков (рис. 1).
Рис. 1 – Визуализация результатов моделирования участка топографической поверхности на регулярной сети точек
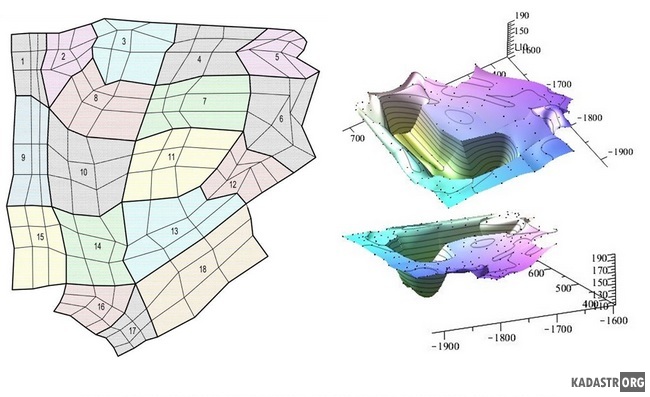
На втором примере [9] показано построение ЦМР, расположенной в верховьях балки Каменская (г. Лисичанск), построенной на нерегулярной сети точек. На рисунке 2 представлена исходная план-схема участка, состоящая из 18-ти 16-точечных отсеков и визуализация полученной модели поверхности. Как видно из рисунка 3, все 16-точечные отсеки носят незакономерный характер. Заметим, что в случае, когда отсек состоит из количества точек менее 16, то без потери общности некоторые точки можно сделать кратными.
Рис. 2 – Визуализация результатов моделирования участка топографической поверхности на нерегулярной сети точек
Также предложенный вычислительный алгоритм может быть эффективно использован для реконструкции ЦМР на основе спутниковых снимков дистанционного зондирования земной поверхности (рис. 3).
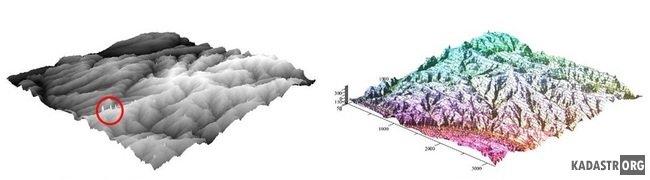
Рис. 3 – Сравнение результатов моделирования ЦМР на основе спутниковых снимков SRTM
На рисунке 3 хорошо видно, что модель, полученная средствами ArcGIS (слева) на основе триангуляции, имеет резкие неконтролируемые всплески высот, что приводит к необходимости дополнительной обработки результатов моделирования. Этих недостатков лишена ЦМР, состоящая из 4356 регулярных 16-точеных отсеков (справа).
Библиографический список
| ||||||||
 |  |
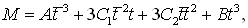
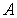и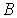 
− начальная и конечная точки дуги кривой Безье 3-го порядка;
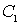и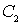 
− точки, определяющие положение касательных в начальной и конечной точках.
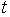− текущий параметр.
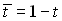− дополнение параметра до 1.
, 
, 
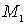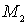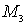и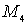 
, получим:
#menuinclude(1-elibraryru)