 |  | ||||||||||||||||
|
УДК 004.942:528.2/.3 Разработка программного продукта на языке Python для моделирования геодинамических явлений методом Христова
Долгий П.С., аспирант Полоцкий государственный университет
Геодинамические явления происходят непрерывно на всей планете и подразделяются на глобальные (движение полюсов Земли), крупномасштабные (движение литосферных плит), а также региональные и локальные, связанные с изменением местоположения и вариациями силы тяжести относительно небольших участков земной коры [1]. Цель данной работы - разработка программного продукта для моделирования геодинамических процессов по результатам повторного нивелирования. В работе будет уделено внимание исследованию локальных современных вертикальных движений земной коры. Для исследования локальных движений земной коры используют такие геодезические методы как повторное нивелирование, повторные линейно-угловые измерения, повторные спутниковые наблюдения. Способом, предоставляющим наиболее точные сведения о вертикальных движениях точек земной поверхности, остается повторное высокоточное нивелирование [2]. Современные исследования в геодинамике требуют комплексного междисциплинарного подхода. Важнейшие инструменты исследования в геодинамике – методы математического моделирования и информационные технологии [3]. Метод, используемый для моделирования современных вертикальных движений земной коры во времени основан на алгебраических полиномах и назван в честь болгарского геодезиста Владимира Христова. Функция алгебраического полинома для линейной аппроксимации приобретает следующий вид
Для квадратичной аппроксимации:
Для кубической аппроксимации:
Для определения коэффициентов H(0), V, A, B составляется система уравнений – одно уравнение для каждого измеренного превышения в каждую эпоху. Этим уравнениям придают веса P, определяемые как величины, обратно пропорциональные длине секций:
C – постоянная, равная отношению априорной погрешности единицы веса к погрешности на 1 км хода; В результате получают систему нормальных уравнений, которую решают по формуле
Прибавляя полученные значения поправок к приближенным высотам пунктов, получают уравненные высоты на начальную эпоху
Подставляя полученные значения скорости, ускорения и производной ускорения в уравнения, получают модельные значения высот на каждую эпоху. Вычитая модельные высоты смежных пунктов хода, получают модельные превышения. Из вычисленных модельных значений высот вычитают полученные по результатам измерений. Среднеквадратическую ошибку модели вычисляют по формуле
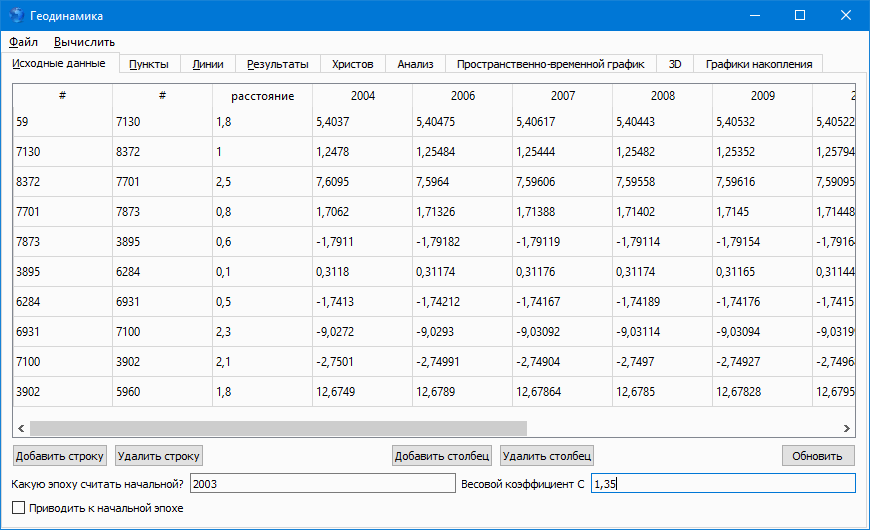
На данный момент для моделирования современных вертикальных движений земной коры используется программный продукт ДК СВДЗК, разработанный в Полоцком государственном университете в 2008 году [6]. Этот продукт имеет высокую скорость вычислений, однако не имеет возможности выполнения кубической аппроксимации, модулей анализа и графического представления результатов. Исходный код продукта к настоящему времени утерян, поэтому было решено выполнить разработку подобного программного продукта заново. Для реализации продукта выбран язык программирования python версии 3.3. Язык является современным, в настоящий момент, согласно различным рейтингам [7,8,9,10], входит в пятерку наиболее популярных в мире. Разработку значительно упрощают лаконичность языка, широкое использование таких производительных языковых конструкций, как генераторы, лямбда-функции и другие, многофункциональная стандартная библиотека, а также возможность простой установки дополнительных модулей. Графические интерфейс пользователя разрабатывался на основе фреймворка PyQt5 (рис. 1). По сравнению с другими фреймворками графического интерфейса для языка Python (PySide, Tkinter, wxWidgets) PyQt5 имеет наиболее полный набор графических элементов, наиболее полную документацию, хорошо описан в технической литературе. Разработчиком PyQt5 является компания Riberbank Computing. Продукт имеет лицензию GPL, которая предоставляет пользователю право копировать, модифицировать и распространять программы, а также гарантировать, что и пользователи всех производных программ получат вышеперечисленные права, при этом запрещая создавать на основе свободной программы под GPL другой проект, не предоставляя его исходники пользователям [11].
Рис. 1 – Интерфейс программного продукта
Для расчетов использовалась библиотека numpy. Данная библиотека, написанная на C, предназначена для научных вычислений. Библиотека не позволяет создавать коллекции данных с различными типами, как в “сыром” Python, следовательно, не требуется проверка типов при операциях с этими данными и производительность возрастает в разы [12]. В разработанном нами программном продукте библиотека numpy использовалась не только для сложных операций, таких как умножение и обращение матриц, но и для более простых, например, вычисление суммы массива [13]. Для визуализации расчетов использована библиотека matplotlib. Данная библиотека имеет возможность как отображать построенные изображения в отдельном окне, так и встраивать их в окна различных фреймворков графического интерфейса python [14]. Для написания кода использовалась интегрированная среда разработчика JetBrains PyCharm edu, являющаяся самой совершенной средой разработки на языке python, поддерживающая подсветку синтаксиса, автодополнение и т.д. Интерфейс программного продукта реализован при помощи вкладок. На первой вкладке выполняется ввод либо импорт исходных данных с возможностью редактирования. Далее необходимо выбрать исходный пункт и ввести его высоту. После выполнения расчетов в окне программы отображаются высоты и превышения, вычисленные по методу Христова, разность между вычисленными и измеренными значениями, а также графическое представление результатов – пространственно-временные графики движения пунктов нивелирования в двумерном и трехмерном виде, графики накопления разностей превышений, а также графики поведения каждого из реперов в отдельности. Отладка программного продукта выполнялась на основе реальных измерительных данных Полоцкого геодинамического профиля, расположенного к северо-западу от г. Полоцк. В данной работе использовались данные 10 циклов (с 2004 по 2015 годы за исключением 2005 и 2014) высокоточного нивелирования на 11 нивелирных пунктах (1 исходный). Таким образом, исходные данные были представлены 100 измерениями [15]. Прибавив вычисленные поправки к полученным по результатам измерений высотам, получили уравненные высоты на эпоху 2003 года (формула (6)). Подставив полученные высоты и значения коэффициентов в формулы (1 – 3), вычислили модельные значения высот. Вычитая модельные значения высот конечных пунктов для каждой линии из высот начальных пунктов, получили модельные превышения. Далее сравнили модельные значения высот с измеренными. По формуле (7) нашли среднюю квадратическую ошибку (СКО) для каждой модели. Значения, которые превышают двойную СКО, не согласуются с моделью с вероятностью 95%.
Таблица 1. - Характеристики различных моделей, описывающих движение нивелирных пунктов Полоцкого геодинамического профиля.
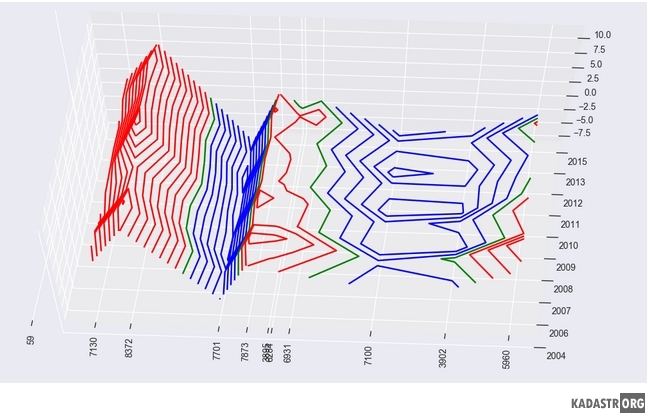
Можно заметить, что с увеличением степени аппроксимации уменьшается число несогласующихся значений. Также примечательно, что во всех трех моделях наибольшее количество несогласующихся значений приурочены к реперу 8372, что, скорее всего, объясняется существованием тектонических разломов по обе стороны от него [15]. Это также подтверждается и на пространственно-временном графике (рис. 2). Далее мы рассмотрели накопление разностей превышений для различных моделей. В одних и тех же координатных осях строились два графика: для измеренных значений и для модельных. Рассматривая два графика, можно понять, насколько хорошо согласуется модель с измеренными значениями. Изучив графики для разностей между различными эпохами, мы выяснили следующее:
Рис 2. – Пространственно-временной график движения нивелирных пунктов Полоцкого геодинамического профиля в трехмерном виде. Синим цветом обозначены отрицательные значения, красным – положительные, зеленым – нулевые.
Несмотря на то, что среднеквадратическая ошибка кубической аппроксимации наименьшая среди всех моделей, а графики накопления разностей превышений наилучшим образом согласуются с измеренными значениями, можно сделать вывод, что кубическая модель наилучшим образом описывает движение нивелирных пунктов. Однако такой вывод нельзя считать окончательным. Необходимо продолжить исследование при наличии большего количества эпох измерений.
Библиографический список
| |||||||||||||||||
 |  | ||||||||||||||||
#menuinclude(1-elibraryru)
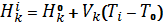 (1)
(1)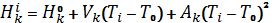 (2)
(2)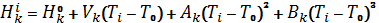 (3)
(3)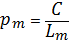 ; (4)
; (4)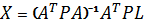 (5)
(5)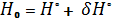 (6)
(6)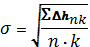 ; (7)
; (7)