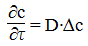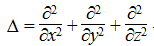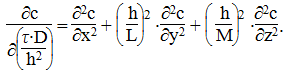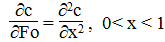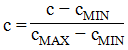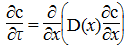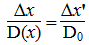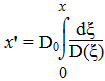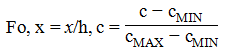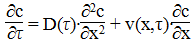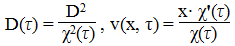Какую пользу могут принести методы подобия при моделировании природных явлений с помощью параболических уравнений

Рассмотрены особенности применения методов подобия для задач математического моделирования процессов тепло-массообмена природных объектов.

Параболические уравнения описывают довольно широкий круг природных явлений, прежде всего таких, где перенос массы-энергии происходит вследствие разности некоторых потенциалов.

Традиционно, например [1], перед решением таких уравнений они (уравнения, краевые условия) предварительно преобразуются к "безразмерному" виду с применением так называемых "методов подобия".

Основной достигаемый при этом результат - получаем "универсальную" математическую модель, которая описывает целую группу "подобных" систем (две системы ведут себя подобным образом, если эти две системы геометрически подобны и если отношения всех существенных для данного процесса сил, энергий и физических свойств одинаковы в этих системах [2]).

Какие еще получаем бонусы:

1. Уменьшение размерности решаемых уравнений.

Поясним на примере. Процесс массопереноса в замкнутом водоеме может быть описан уравнением вида

(1)

где с(x, y, z, τ) - концентрация исследуемого вещества,
D - коэффициент диффузии вещества в воде,

- оператор Лапласа

Считаем:

ось Ox направлена вертикально,

h - максимальная глубина водоема,

L, M - его длина и ширина вдоль осей Oy и Oz.

В процессе нормализации произведем замену x = x/h, y = y/L, z = z/M, и получим новое уравнение

(2)

Если глубина водоема (h) не превышает 10 м, а длина и ширина не меньше 1000 м, то (h/L)² и (h/M) ²2 будут иметь порядок 10 ^-4 - 10 ^-5. Следовательно, без особой потери точности модели в уравнении (2) можем просто пренебречь соответствующими членами.

В результате имеем уравнение

(3)

где F₀ = τD/h² - называют числом Фурье или безразмерным временем.

То есть сразу переходим от трехмерного уравнения к одномерному.

В (3) еще остается размерная величина - с(x, F₀), и ее нормализация выполняется заменой

где с_MIN и с_MIN определяются из краевых условий исходной задачи в соответствии с принципом максимума [3].

2. Если задачу решаем численными методами, например, при помощи разностных схем, то для уравнения вида (3) существенно упрощается исследование этих схем на устойчивость и сходимость, оценка точности аппроксимации - большинство работ на эту тему (например, [4]) посвящены именно таким уравнениям. Можно легко подобрать безусловно устойчивую разностную схему с достаточной точностью аппроксимации.

3. Большинство сред, в которых происходят процессы, моделируемые уравнением (1), являются многослойными. То есть фактически D = D(x), а на границах раздела сред задаются специальные условия сопряжения (условия неразрывности потока массы/тепла).

Однако, если применить метод дифференциального подобия [5], из уравнение вида

легко получить уравнение вида (3) и, тем самым еще больше расширить область применения алгоритмов, автоматизирующих поиск решения поставленной задачи.

Суть метода дифференциального подобия - специальная деформация области решения вдоль оси Ox.

Деформация определяется соотношением

которое определяет условия замены среды толщиной Δx с коэффициентом диффузии (теплопроводности) D(x) слоем толщиной Δx' и с коэффициентом D₀ = const.

В результате координаты x исходного отрезка, где D = D(x), преобразуются в новые координаты

При этом D(x') = D₀ .

4. Экспериментальное подтверждение результатов моделирования, основанное на уравнении (3), позволяет не обращать внимания на природу конкретных явление, если выполняется главное условие - экспериментатор сохраняет соотношения между параметрами, образующих безразмерные комплексы:

и т.п.

Например, исследование процессов массопереноса легко заменяется аналогичными (подобными) экспериментами по распространению тепла (и наоборот).

Не смотря на привлекательность рассмотренных выше приемов нормализации, у них есть и ограничения:

• полученные решения дают представление о качественном поведении исследуемых процессов - для того, чтобы перейти к реальным (размерным) величинам, требуется выполнить обратные преобразования. Что требует дополнительных затрат (время, дополнительные алгоритмы/программы и т.п.);
  
• существует ряд задач, для которых нецелесообразно получать полностью безразмерные уравнения, так как не существует характерных параметров (аналоги h, L, M, с_MIN, с_MIN, D₀), которые можно использовать для этих целей.
  

Например, "простое" усложнение краевых условий для уравнения (1),

когда верхняя граница водоема изменяется по произвольному закону χ(τ).

В результате подстановки x = x/ χ(τ) получаем уравнение вида



Здесь переменная x - уже не имеет размерности и лежит в интервале [0; 1], с(x, τ) - приводим к безразмерному виду, как описано выше,

остаются с размерностью [время[sup]1].

Для практических нужд (выбор разностной схемы, ее программная реализация, исследование полученных результатов) оказалась ненужной "полная" нормализация уравнения - было бы трудно интерпретировать физический смысл полученных безразмерных комплексов.

Таким образом, в большинстве случаев методы подобия дают универсальные модели процессов, и как следствие, алгоритмы их исследования. Однако они (методы) не могут быть применены абсолютно ко всем задачам, что оставляет исследователям возможности для творческой самореализации.

Библиографический список

1. Лыков А.В. Теория тепло- и массопереноса / М.: Гос. энерг. изд-во, 1963. - 535 с.
   
2. Клайн С.Дж. Подобие и приближенные методы / М.: Мир, 1968. - 302 с.
   
3. Тихонов А.Н., Самарский А.А. Уравнения математической физики / М.: Гос. изд-во техн.- теор. лит-ры, 1953. - 679 с.
   
4. Самарский А.А. Теория разностных схем / М.: Наука, 1989. - 614 с.
   
5. Исследования по теплопроводности / Под ред. Лыкова А.В. - Минск: Наука и техника, 1967. - 575 с.
   

1. Государственный кадастр недвижимости и земельно-имущественные отношения
   
2. Мониторинг природных ресурсов и охрана окружающей среды
   
3. Комплексное использование природных ресурсов
   
4. Современные вопросы геологии
   
5. Физика горных пород
   
6. Новые технологии в природопользовании
   
7. Применение современных информационных технологий
   
8. Экономические аспекты недвижимости
   
9. Мониторинг использования объектов недвижимости
   
10. Топографо-геодезическое обеспечение кадастровых работ