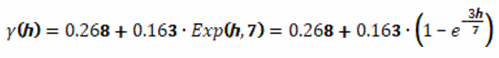 |  | |||
|
УДК 519.24 Геостатистический подход к анализу гидроэкологических данных
Цеховая Т.В., доцент Белорусский государственный университет, Белоруссия
Рассмотрен временной ряд средних значений растворимости кислорода в водах озера Баторино (Беларусь) в августе месяце с 1966 по 2012 гг. Первичная обработка, статистический анализ и прогнозирование данных выполнены с помощью языка программирования Python.
Работа посвящена применению геостатистического подхода для прогнозирования реального временного ряда, представляющего собой средние значения растворимости кислорода в водах озера Баторино (Беларусь) в августе месяце с 1966 по 2012 годы на горизонте 3 м. База данных предоставлена учебно-научным центром «Нарочанская биологическая станция им. Г.Г. Винберга». Для решения поставленной задачи был выбран современный высокоуровневый язык программирования Python. В процессе первичного анализа исследуемой выборки были вычислены основные описательные статистики. Среднее значение растворимости кислорода оказалось равным 8.74, выборочная дисперсия - 0.43. Коэффициент вариации равен 7.55%, что означает однородность исходных данных. По полученным значениям коэффициентов асимметрии (As = – 0.32) и эксцесса (Ex = – 0.83), можно сделать вывод о незначительной левосторонней асимметрии и пологости кривой выборочного распределения относительно нормального закона. Статистические тесты Колмогорова-Смирнова и Шапиро-Уилка при уровне значимости α = 0.05 отвергают гипотезу о нормальном законе распределения с параметрами 𝑁(8.74, 0.43) исследуемых данных. Критерий Фостера-Стюарда отвергает нулевую гипотезу о существовании тренда. Статистический тест Дики-Фуллера подтверждает стационарность исследуемого ряда. С учетом результатов работы [1] проведен вариограммный анализ растворимости кислорода. Построена классическая оценка семивариограммы и визуальным методом подобраны шесть моделей семивариограммы: линейная модель с порогом, линейная модель с порогом и эффектом самородка, три экспоненциальные модели с различными параметрами и модель Гаусса. Поскольку между элементами исследуемой выборки логично предположить зависимость на расстояниях, меньших чем расстояние между наблюдениями, было принято решение включить в некоторые модели семивариограммы ненулевой эффект самородка. Далее методом обычного кригинга, в основе которого лежат построенные модели семивариограммы, осуществлено прогнозирование значений и вычисление дисперсий ошибок. График дисперсий представлен на рисунке 1.
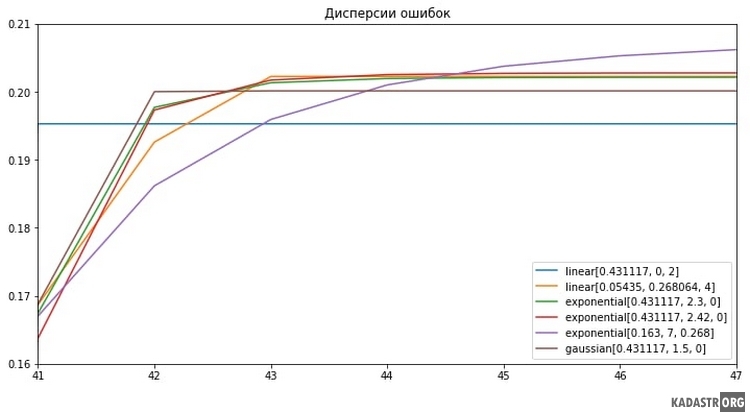
Рис. 1 – Дисперсии ошибок прогнозов, полученных методом обычного кригинга
Как видно из рисунка экспоненциальная модель с эффектом самородка имеет наименьшие значения дисперсий ошибок в начале, однако с увеличением расстояния, дисперсия увеличивается. Указанная модель определяется равенством (2).
На втором месте находится линейная модель с порогом и эффектом самородка. Для построения долгосрочных прогнозов лучше использовать линейную модель, поскольку на больших расстояниях она имеет меньшую дисперсию, чем другие модели. Однако следует отметить, что у всех исследуемых моделей значения дисперсий ошибок очень близки.
Библиографический список
| ||||
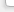 |  |