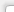 |  | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
УДК 528.63 Сравнение элементов преобразования при разных способах реализации вычислительного алгоритма их получения
Дегтярёв А.М., доцент, Ивашнёва А.С., аспирант Полоцкий государственный университет, Беларусь
Проведено сравнение элементов преобразования, полученных при разных способах реализации вычислительного алгоритма их получения, а именно когда в процессе вычислений производные берутся по коэффициентам или по элементам (модель трансформирования известна). Вычислительный эксперимент проведен с использованием аффинной и конформной моделей при нескольких вариантах расположения общих точек.
Необходимость преобразования координат возникает, когда координаты геодезических точек вычисляют в различных координатных системах. На сегодняшний день необходимость в данной процедуре растет, это связано с ростом количества и качества информации и необходимостью интегрирования данных из разнородных источников. Двумерное трансформирование очень часто является достаточным для решения подавляющего числа задач на преобразование систем координат. В большинстве практических случаев задача такого рода решается, когда часть сети вставляется в сеть с другой системой координат; когда определяются элементы деформации различных объектов; когда главные оси объектов включаются в государственную систему; в фотограмметрических работах; в географических информационных системах, при выполнении кадастровых работ и т.д.
Преобразование координат из одной системы в другую может быть
где a1, b1, c1, a2, b2, c2 - преобразующие коэффициенты; XH,YH -координаты общей точки в старой системе; XC,YC - координаты этой же точки в новой системе. В зависимости от того какими элементами преобразования представлено трансформирование выделяют следующие традиционные модели планового преобразования координат: твердотельные, конформные, ортогональные, аффинные. Всего существует шесть элементов двумерного преобразования, которые могут участвовать в трансформировании координатных систем: tx – сдвиг по оси X, ty – cдвиг по оси Y, φ – угол поворота осей одной координатной системы относительно другой, mх – величина изменения масштаба по оси X, mу – величина изменения масштаба по оси Y, ε – угол неортогональности между осями двух координатных систем. В зависимости от того, какая модель преобразования, в коэффициентах будет содержаться определенный набор элементов. В конформной модели выполняется равномерный разворот всех точек на угол φ, сдвиги по осям на величины tx и ty и равномерно изменяется масштаб на величину m по формулам:
В аффинной модели производиться сдвиг по осям на величины tx и ty, изменяется масштаб на величины mх и mу, выполняется поворот относительно одной оси на угол φ1, а другой, на угол φ2 = φ1 + e, т.е. с нарушением ортогональности исходной системы координат, по формулам:
В ходе вычислительного эксперимента стояла задача получить и сравнить элементы преобразования, полученные по способу трансформирования, основанному на производных по коэффициентам, [2] и по способу трансформирования, основанному на производных по элементам [3]. Для реализации данных способов использовалась аффинная и конформная модели. Вычислительный эксперимент проведен по трем вариантам расчета: -по аффинной модели преобразования, при условии, что производные берутся по коэффициентам. Учитывается, что алгоритм аффинных преобразований дает совершенно идентичные результаты для любых других видов преобразований, если в них отсутствуют не свойственные им параметры и погрешности координат. То есть, используя аффинные преобразования для случая, когда они точно конформные, мы должны получить результаты, идентичные результатам алгоритма конформных преобразований; -по конформной модели преобразования, при условии, что производные берутся по коэффициентам; -по конформной модели преобразования, при условии, что производные берутся по элементам преобразования. Для вычислительного эксперимента координаты десяти точек преобразовывались в другую систему по известным (заранее заданным) элементам конформной модели трансформирования:
Полученные таким образом две системы координат искажались случайными ошибками. По двум испорченным системам координат вычислялись элементы аффинного и конформного преобразования, и проводилось их сравнение с изначально заложенными элементами преобразования. При этом данные алгоритмы вычислений повторялись при различных вариантах расположения десяти точек. Варианты расположения общих точек, по которым проводились расчеты, представлены на Рисунке 1.
Рис.1 – Геометрия расположения точек A), B), C), D)
Результаты по трем вариантам реализации алгоритма вычисления элементов преобразования представлены в таблице 1, таблице 2 и таблице 3, соответственно. Очевидно, что при изменении вида модели трансформирования соответственно будет меняется состав элементов преобразования (аффинная модель – шесть элементов преобразования, конформная модель – четыре элемента преобразования). Также вычислены отклонения полученных элементов преобразования от изначально заложенных элементов. Результаты представлены в таблице 4, таблице 5 и таблице 6.
Таблица 1 - Вычисленные элементы преобразования по аффинной модели (производные по коэффициентам преобразования)
Таблица 2 - Вычисленные элементы преобразования по конформной модели (производные по коэффициентам преобразования)
Таблица 3 - Вычисленные элементы преобразования по конформной модели (производные по элементам преобразования)
Таблица 4 - Отклонения вычисленных элементов преобразования по аффинной модели от заложенных элементов преобразования (производные по коэффициентам)
Таблица 5 - Отклонения вычисленных элементов преобразования по конформной модели от заложенных элементов преобразования (производные по коэффициентам)
Таблица 6 - Отклонения вычисленных элементов преобразования по конформной модели от заложенных элементов преобразования (производные по элементам преобразования)
На основе полученных данных, можно сделать вывод о том, что два способа решения задачи трансформирования, когда производные берутся по коэффициентам и по элементам преобразования, дают одинаковые результаты (при одной модели преобразования). При этом алгоритм с производными по коэффициентам обладает простым ходом вычислений, в отличии от алгоритма с производными по элементам, где решение получается методом итераций. Проанализировав изменения элементов преобразования по трем алгоритмам вычисления, следует отметить, что по мере приближения к наихудшей геометрии расположения общих точек наиболее устойчивой моделью является конформная модель.
Библиографический список
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 |  |
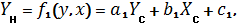
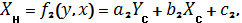 (1)
(1)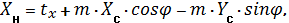
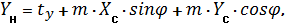 (2)
(2)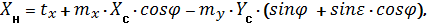
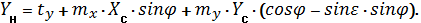 (3)
(3)