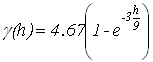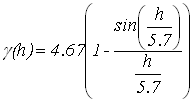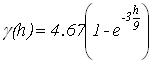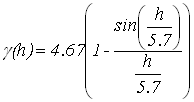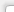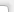 |  | |||||||||||||||||||||||||
 УДК 004 Геостатистический анализ батиметрических данных
Смирнова В.А., студентка Научный руководитель: Цеховая Т.В., доцент Белорусский государственный университет, Беларусь
Спрогнозированы значения глубин озера Мертвое в ненаблюдаемых точках с помощью геостатистического метода прогнозирования кригинг. Построены изолинии и поверхность дна озера.
Задачи геостатистики очень актуальны в настоящее время. Современная геостатистика быстро развивается и ее спектр весьма широк – от традиционного использования в области добычи природных ископаемых до использования в экономике, финансах, экологии, почвоведении и многих других естественных и социальных науках. Предметом анализа геостатистики являются, например, пространственные переменные: количество осадков, плотность загрязнения почвы, плотность населения в некоторой географической области. Вариограмма является основным инструментом анализа пространственной связи. Кригинг – основная интерполяционная модель геостатистики. Он является основой всех методов, связанных с геостатистикой,– интерполяции, вероятностного картирования, стохастического моделирования. Работа посвящена прогнозированию геостатистическим методом кригинг значений глубин озера в ненаблюдаемых точках с помощью пакета R. От научно-исследовательской лаборатории озероведения географического факультета Белорусского государственного университета были получены промеры глубин озера Мёртвое (Беларусь). Озеро находится в Мядельском районе Минской области, входит в группу Голубые озёра. Наблюдения снимались в двух направлениях – север-юг и запад-восток. В направлении север-юг 53 наблюдения, в направлении запад-восток 98 наблюдений. Проведен первичный анализ исходных данных. Средняя глубина озера 6.4 метра, максимальная глубина – 10.3 метра. При исследовании данных на выбросы получено, что выбросы присутствуют, но из рассмотрения они не удаляются, т.к. это значения являются глубинами, измеренными около берега. При исследовании на стационарность получено, что выборочная нормированная ковариационная функция является колебательной и постепенно затухает, что говорит о стационарности данных в шикором смысле. Семивариограмма является основой геостатистических методов. На практике для данных строится оценка семивариограммы, которая известна в дискретных точках, а для прогнозирования геостатистическими методами нужна непрерывная семивариограмма, поэтому к полученной оценке семивариограммы подбирается модель. Воспользуемся оценкой семивариограммы, введённой Ж.Матероном, которая называется классической [1]. С помощью пакета R построены оценки семивариограмм по направлениям север-юг, запад-восток. Для этого используется функцией vario() из пакета pastecs. Модель семивариограммы подбирается так, чтобы она соответствовала оценкам семивариограммы по направлениям одновременно. Поскольку гипотеза о стационарности для обобщенных данных подтвердилась, то подбраны различные пороговые модели семивариограмм. Для модели семивариограммы нужно указать порог и ранг. В качестве порога берется дисперсия для обобщенных данных, которая равна 4.67. Для более точного определения ранга модели построены диаграммы разброса для обобщенных данных. По диаграммам разброса берется ранг равный 9. Также выбран ранг, исходя из выборочной нормированной ковариационной функции для обобщенных данных. Так как наша выборочная нормированная ковариационная функция является колебательной, то в качестве ранга берется 12[2]. Разместим построенные оценки семивариограмм по направлениям на одной координатной плоскости. Для подбора модели семивариограммы используется визуальный метод. Рекомендовано, чтобы модель семивариограммы повторяла поведение в окрестности нуля. С полученными рангами рассмотрены экспоненциальная, сферическая, гауссова модели семивариограмм. Так как в направлении запад-восток наблюдается квадратичный тренд, то интересно отдельно рассмотреть модель семивариограммы с эффектом дырок. Для подбора модели используется функция vgm() из пакета gstat. Параметрами функции vgm() являются модель семивариограммы, порог, наггет эффект. В качестве параметра модели семивариограммы рассматриваются значения Gau(гауссова модель), Exp(экспоненциальная модель), Sph(сферическая модель), Hol(модель с эффектом дырок). Выбран ранг для модели семивариограммы с эффектом дырок из визуального сравнения. В качестве ранга для этой модели берется 5.7. Для применения метода кригинг использована функция krige() из пакета gstat. Главным параметром этой функции является модель семивариограммы. Применен метод кригинг ко всем полученным моделям семивариограммы. Определена лучшая модель семивариограммы для прогнозирования. Поскольку метод кригинг заключается в минимизации дисперсии ошибки прогнозирования, поэтому проведено сравнение по дисперсиям ошибок. Найдены выборочные характеристики для полученных дисперсий ошибок.
Таблица 1 - Характеристики для дисперсий ошибок
Рассмотрим таблицу. Минимальное среднее значение получаем у модели с эффектом дырок
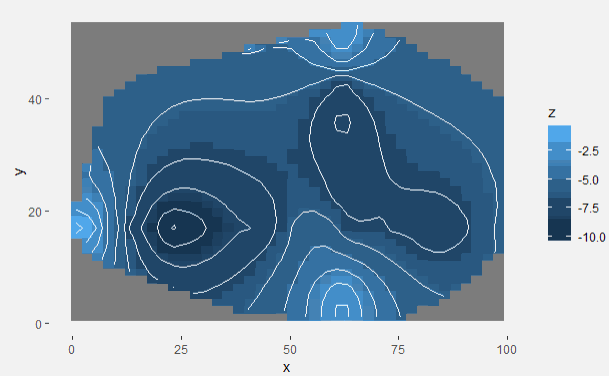
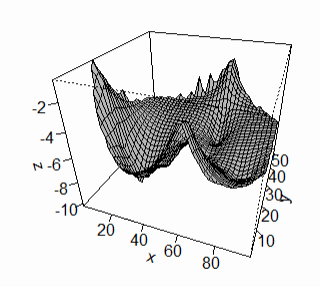
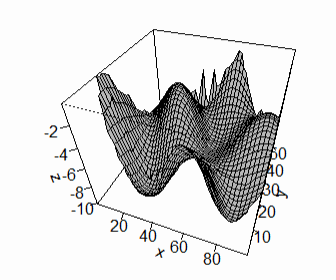
Получено, что лучшими моделями семивариограммы являются экспоненциальная модель Используя возможности R[3], построены изолинии и поверхность дна озера, полученную с помощью метода прогнозирования кригинг.
Рис. 1 - 2D изолинии поверхности дна озера, построенного с экспоненциальной моделью семивариограммы
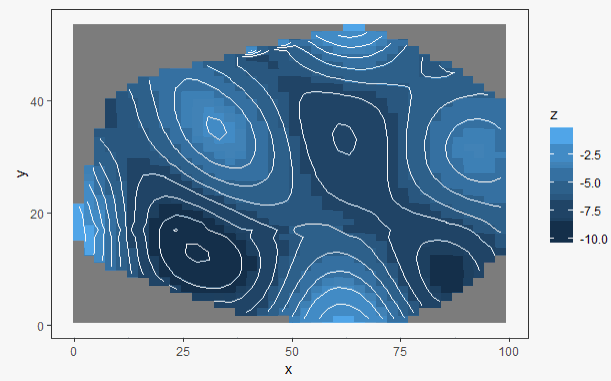
Рис. 2 - 2D изолинии поверхности дна озера, построенного с моделью семивариограммы с эффектом дырок
Рис. 3 - 3D график поверхности дна озера, построенного с экспоненциальной моделью семивариограммы
Рис. 4 - 3D график поверхности дна озера, построенного с моделью семивариограммы с эффектом дырок
Библиографический список
| ||||||||||||||||||||||||||
 |  |
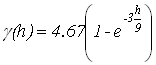
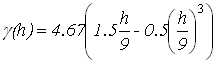
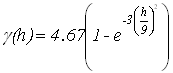
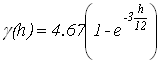
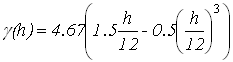
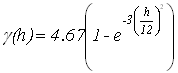
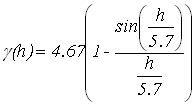
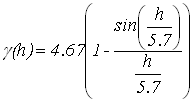, минимальная дисперсия – у экспоненциальной модели 
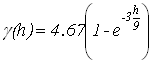. Минимальную дисперсию экспоненциальной модели можно объяснить тем, что области с плохой обеспеченностью данными заполняются плавно.
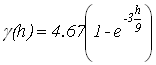и модель с эффектом дырок 
.
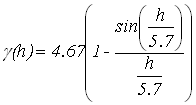#menuinclude(1-elibraryru)